首页 物理 量子 量子力学

# 波函数

# Schrödinger 方程

假设质量为 mm 的粒子沿 xx 轴运动，所受的力为 F(x,t)F(x,t) 。在经典力学中我们会根据牛顿定律写出微分方程，根据初始条件求出 x(t)x(t) ，从而确定任何一个动力学量。在量子力学中，我们寻找的是波函数， Ψ(x,t)\Psi(x,t)，而得到波函数则需要通过解 Schrödinger 方程：

iℏ∂Ψ∂t=−ℏ22m∂2Ψ∂Ψ∂x2+VΨi\hbar\frac{\partial\Psi}{\partial t}=-\frac{\hbar^2}{2m}\frac{\partial^2\Psi}{\partial\Psi}{\partial x^2}+V\Psi

其中 i2=−1i^2=-1 ，ℏ=h2π=1.5457182×10−34\hbar=\frac{h}{2\pi}=1.5457182\times10^{-34} J⋅\cdots

# 波函数的统计诠释

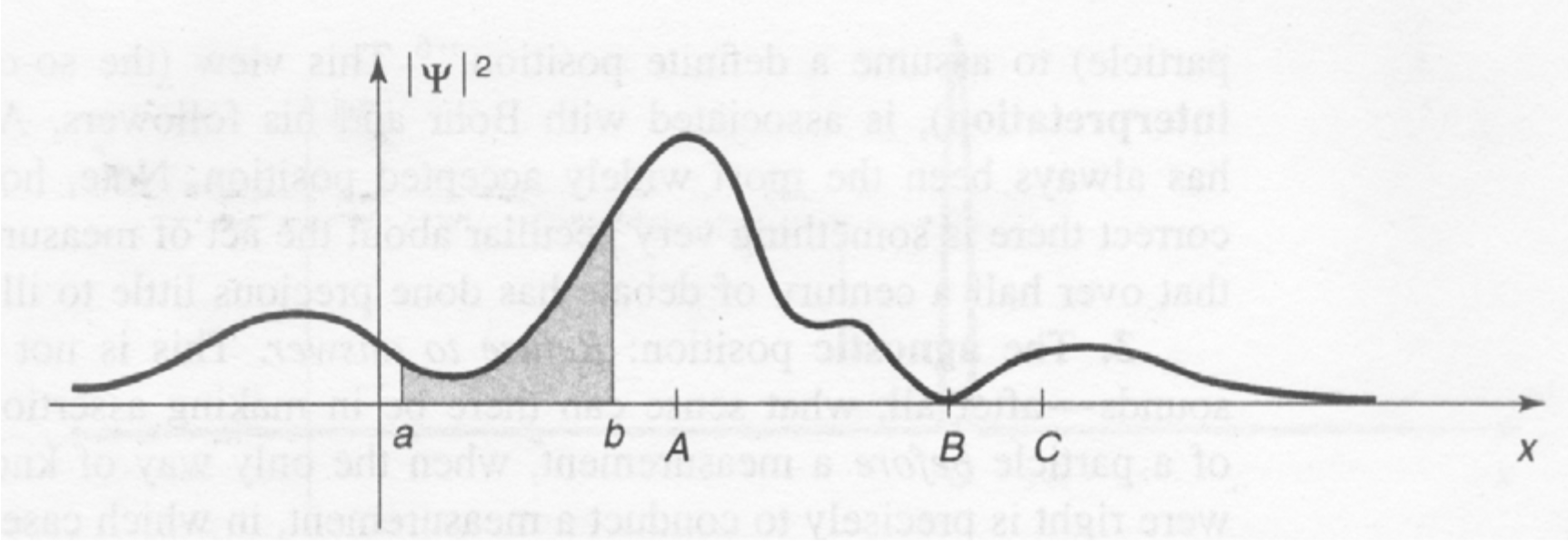
波恩 (Born) 关于波函数的统计诠释指出 ∣Ψ(x,t)∣2\lvert\Psi(x,t)\rvert^2 给出在时刻 tt 在 xx 处发现这个粒子的概率，即：

∫ab∣Ψ(x,t)∣2dx={在t时刻发现粒子处于区间a到b的概率}\int_a^b\lvert\Psi(x,t)\rvert^2dx=\{在t时刻发现粒子处于区间a到b的概率\}

在粒子被探测到之前它在哪呢？这个问题催生了不同的派系。1964 年 John Bell 宣布粒子在测量前有没有在一个确切的位置会导致不同的测量结果。现在实验已经决定性地证明了正统观点：一个粒子在测量前没有一个确定的位置。

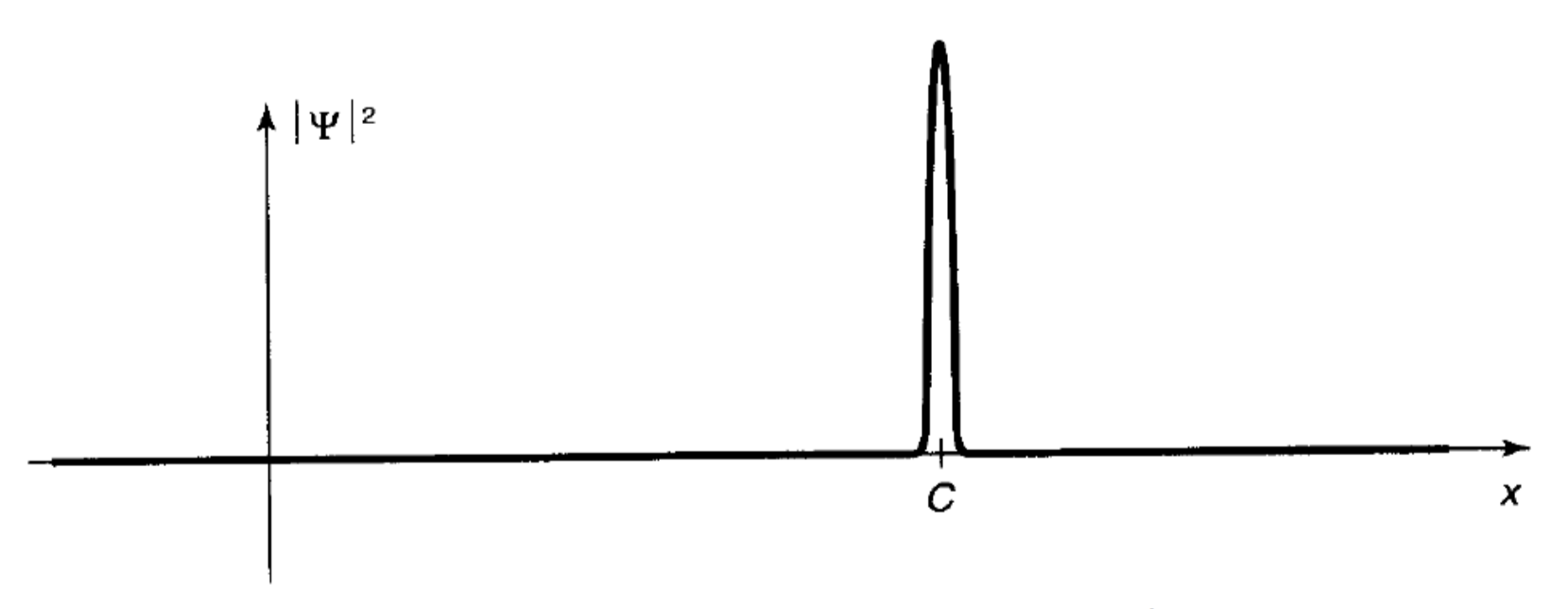
测量会完全改变波函数，导致波函数的坍塌。

几率

⟨j⟩\langle j\rangle 代表 jj 的平均值。

⟨Δj⟩=∑(j−⟨j⟩)P(j)=∑jP(j)−⟨j⟩∑P(j)=⟨j⟩−⟨j⟩=0.\langle \Delta j \rangle = \sum (j - \langle j \rangle) P(j) = \sum j P(j) - \langle j \rangle \sum P(j) = \langle j \rangle - \langle j \rangle = 0.

方差：

σ2≡⟨(Δj)2⟩.\sigma^2 \equiv \left\langle (\Delta j)^2 \right\rangle.

很简单推出关系：

σ2=⟨j2⟩−⟨j⟩2\sigma^2=\langle j^2\rangle-\langle j\rangle^2

# 归一化

统计诠释指出 ∣Ψ(x,t)∣2\lvert\Psi(x,t)\rvert^2 是 tt 时刻发现粒子在 xx 的几率密度，则 ∣Ψ∣2\lvert\Psi\rvert^2 须为 1，即粒子一定在空间某处：

∫−∞∞∣Ψ(x,t)∣2dx=1\int_{-\infty}^{\infty} \lvert\Psi(x, t)\rvert^2dx = 1

故可以在波函数前添加系数来使其归一化。不能归一化的解是不能描述粒子的，比如积分无穷大和 Ψ=0\Psi=0 的平庸解，应该舍弃。

波函数随时间演化保持归一化

计算

ddt∫−∞∞∣Ψ(x,t)∣2dx=∫−∞∞∂∂t∣Ψ(x,t)∣2dx.\frac{d}{dt} \int_{-\infty}^{\infty} |\Psi(x,t)|^2 \, dx = \int_{-\infty}^{\infty} \frac{\partial}{\partial t} |\Psi(x,t)|^2 \, dx.

（注意积分后仅是 tt 的函数，所以在第一个表示式中用了全导数 d/dtd/dt，而被积函数即是 xx 的函数也是 tt 的函数，所以在第二个表示式中用了偏导数 ∂/∂t\partial/\partial t）由求导规则，

∂∂t∣Ψ∣2=∂∂t(Ψ∗Ψ)=Ψ∗∂Ψ∂t+Ψ∂Ψ∗∂t.\frac{\partial}{\partial t} |\Psi|^2 = \frac{\partial}{\partial t} (\Psi^* \Psi) = \Psi^* \frac{\partial \Psi}{\partial t} + \Psi \frac{\partial \Psi^*}{\partial t}.

薛定谔方程可以写作

∂Ψ∂t=iℏ2m∂2Ψ∂x2−iℏVΨ,\frac{\partial \Psi}{\partial t} = \frac{i \hbar}{2m} \frac{\partial^2 \Psi}{\partial x^2} - \frac{i}{\hbar} V \Psi,

及其共轭式

∂Ψ∗∂t=−iℏ2m∂2Ψ∗∂x2+iℏVΨ∗,\frac{\partial \Psi^*}{\partial t} = -\frac{i \hbar}{2m} \frac{\partial^2 \Psi^*}{\partial x^2} + \frac{i}{\hbar} V \Psi^*,

所以

∂∂t∣Ψ∣2=iℏ2m(Ψ∗∂2Ψ∂x2−Ψ∂2Ψ∗∂x2)=∂∂x(iℏ2m(Ψ∗∂Ψ∂x−∂Ψ∗∂xΨ)).\frac{\partial}{\partial t} |\Psi|^2 = \frac{i \hbar}{2m} \left( \Psi^* \frac{\partial^2 \Psi}{\partial x^2} - \Psi \frac{\partial^2 \Psi^*}{\partial x^2} \right) = \frac{\partial}{\partial x} \left( \frac{i \hbar}{2m} \left( \Psi^* \frac{\partial \Psi}{\partial x} - \frac{\partial \Psi^*}{\partial x} \Psi \right) \right).

现在第 1 式积分可以直接写出：

ddt∫−∞∞∣Ψ(x,t)∣2dx=iℏ2m[Ψ∗∂Ψ∂x−∂Ψ∗∂xΨ]−∞∞.\frac{d}{dt} \int_{-\infty}^{\infty} |\Psi(x,t)|^2 \, dx = \frac{i \hbar}{2m} \left[ \Psi^* \frac{\partial \Psi}{\partial x} - \frac{\partial \Psi^*}{\partial x} \Psi \right]_{-\infty}^{\infty}.

但是当 xx 趋于（±）无限大时 Ψ(x,t)\Psi(x,t) 必须趋于零，否则波函数是不可归一化的。这样有

ddt∫−∞∞∣Ψ(x,t)∣2dx=0,\frac{d}{dt} \int_{-\infty}^{\infty} |\Psi(x,t)|^2 \, dx = 0,

因此积分是一个常数（不依赖于 tt），如果 Ψ\Psi 在 t=0t = 0 时是归一化的，它在以后所有时刻保持归一化。证毕。

# 动量

# x 期待值

对于处于 Ψ\Psi 态的粒子来说，其 xx 的期待值为：

⟨x⟩=∫−∞∞x∣Ψ(x,t)∣2dx\langle x\rangle=\int_{-\infty}^{\infty} x |\Psi(x, t)|^2 \, dx

但是每次测量都会导致波函数的坍塌，所以这里的期待值是对含有相同体系的一个系综中不同体系的重复测量的平均值，而不是对同一个体系的重复测量的平均值。

d⟨x⟩dt=∫x∂∂t∣Ψ∣2dx=iℏ2m∫x∂∂x(Ψ∗∂Ψ∂x−∂Ψ∗∂xΨ)dx\frac{d \langle x \rangle}{dt} = \int x \frac{\partial}{\partial t} |\Psi|^2 \, dx = \frac{i \hbar}{2m} \int x \frac{\partial}{\partial x} \left( \Psi^* \frac{\partial \Psi}{\partial x} - \frac{\partial \Psi^*}{\partial x} \Psi \right) dx

利用分部积分公式，上式可以写为

d⟨x⟩dt=−iℏ2m∫(Ψ∗∂Ψ∂x−∂Ψ∗∂xΨ)dx=−iℏm∫Ψ∗∂Ψ∂xdx\frac{d \langle x \rangle}{dt} = -\frac{i \hbar}{2m} \int \left( \Psi^* \frac{\partial \Psi}{\partial x} - \frac{\partial \Psi^*}{\partial x} \Psi \right) dx= -\frac{i \hbar}{m} \int \Psi^* \frac{\partial \Psi}{\partial x} \, dx

此处用到了薛定谔方程。
这样就可以求 xx 期待值的 “速度”，

⟨v⟩=d⟨x⟩dt\langle v\rangle=\frac{d\langle x\rangle}{dt}

# 动量期待值

动量 p=mvp=mv ：

⟨p⟩=md⟨x⟩dt=−iℏ∫(Ψ∗∂Ψ∂x)dx.\langle p \rangle = m \frac{d \langle x \rangle}{dt} = -i \hbar \int \left( \Psi^* \frac{\partial \Psi}{\partial x} \right) dx.

我们还可以把 ⟨x⟩\langle x\rangle 和 ⟨p⟩\langle p\rangle 写成更具启发性的式子：

⟨x⟩=∫Ψ∗(x)Ψdx,\langle x \rangle = \int \Psi^*(x) \Psi \, dx,

⟨p⟩=∫Ψ∗(ℏi∂∂x)Ψdx.\langle p \rangle = \int \Psi^* \left( \frac{\hbar}{i} \frac{\partial}{\partial x} \right) \Psi \, dx.

量子力学中算符 xx “表示” 位置，算符 (ℏ/i)(∂/∂x)\left(\hbar/i\right)\left(\partial/\partial x\right) “表示” 动量；计算期望值时我们把适当的算符放在 Ψ∗\Psi^* 和 Ψ\Psi 之间，然后积分。

其他经典力学量

其他所有经典力学量都可以表示为坐标和动量的函数。例如，动能是

T=12mv2=p22m,T = \frac{1}{2} mv^2 = \frac{p^2}{2m},

角动量是

L=r×mv=r×p\mathbf{L} = \mathbf{r} \times m \mathbf{v} = \mathbf{r} \times \mathbf{p}

（当然，角动量对一维运动不存在）。要计算任何这样的量，Q(x,p)Q(x, p) 的期望值，我们简单地用 (ℏ/i)(∂/∂x)(\hbar/i)(\partial/\partial x) 取代每一个 pp，再把得到的算符放在 Ψ∗\Psi^* 和 Ψ\Psi 之间，然后积分。

⟨Q(x,p)⟩=∫Ψ∗Q(x,ℏi∂∂x)Ψdx.\langle Q(x, p) \rangle = \int \Psi^* Q \left( x, \frac{\hbar}{i} \frac{\partial}{\partial x} \right) \Psi \, dx.

例如，动能的期望值是

⟨T⟩=−ℏ22m∫Ψ∗∂2Ψ∂x2dx.\langle T \rangle = - \frac{\hbar^2}{2m} \int \Psi^* \frac{\partial^2 \Psi}{\partial x^2} \, dx.

# 不确定性原理

对于一个波：波的位置越精确，波长就越不精确，反过来也一样。（类比一般机械波）

德布罗意 (de Broglie) 公式：

p=hλ=2πℏλp=\frac{h}{\lambda}=\frac{2\pi\hbar}{\lambda}

同样适用于波函数。这样波长的弥散对应动量的弥散，对我们通常的观测有：粒子的位置确定的越精确，它的动
量就越不精确。定量上有，

σxσp>=ℏ2\sigma_x\sigma_p>=\frac{\hbar}{2}

其中 sigmaxσpsigma_x \sigma_p 分别是 xx pp 的标准差。这就是海森堡 (Heisenberg) 不确定原理。

这里 “弥散” 是指对全同体系的测量而不会产生同样结果这样一个事实。

# 定态 Schrödinger 方程

# 定态

要得到 Ψ(x,t)\Psi(x,t) 需要解薛定谔方程，这里我们需要根据一个特定的势函数 V(x,t)V(x,t) :

iℏ∂Ψ∂t=−ℏ22m∂2Ψ∂Ψ∂x2+VΨi\hbar\frac{\partial\Psi}{\partial t}=-\frac{\hbar^2}{2m}\frac{\partial^2\Psi}{\partial\Psi}{\partial x^2}+V\Psi

这里假设 VV 是不依赖时间的，即 V(t)V(t) ，用分离变量：

Ψ(x,t)=ψ(x)ϕ(t)\Psi(x,t)=\psi(x)\phi(t)

代入原方程分离变量得：

iℏ1φdφdt=−ℏ22m1ψd2ψdx2+V.i \hbar \frac{1}{\varphi} \frac{d \varphi}{d t} = -\frac{\hbar^2}{2m} \frac{1}{\psi} \frac{d^2 \psi}{d x^2} + V.

此时右边仅为 xx 函数，左边仅为 tt 函数，若等式成立则要求两边同时为常数，设为 EE：

dφdt=−iEℏφ\frac{d \varphi}{d t} = -\frac{i E}{\hbar} \varphi

−ℏ22md2ψdx2+Vψ=Eψ.-\frac{\hbar^2}{2m} \frac{d^2 \psi}{d x^2} + V \psi = E \psi.

第一个方程一般解为 Ce−iEtℏCe^{-i\frac{Et}{\hbar}} ，我们可以把 CC 合并到 ψ\psi 中， ϕ(t)=e−iEtℏ\phi(t)=e^{-i\frac{Et}{\hbar}} 着重研究 ψϕ\psi\phi。
第二个关于 xx 的方程称为定态 (time-independent) 薛定谔方程，求解需要指定 V(x)V(x) 。

这样可以得到：

Ψ(x,t)=ψ(x)−iEtℏ\Psi(x,t)=\psi(x)^{-i\frac{Et}{\hbar}}

而一般波函数是分离变量解的线性叠加：

Ψ(x,t)=∑n=1∞cnψn(x)e−iEnt/ℏ=∑n=1∞cnΨn(x,t)\Psi(x, t) = \sum_{n=1}^{\infty} c_n \psi_n(x) e^{-i E_n t / \hbar} = \sum_{n=1}^{\infty} c_n \Psi_n(x, t)

# 一维无限深方势阱

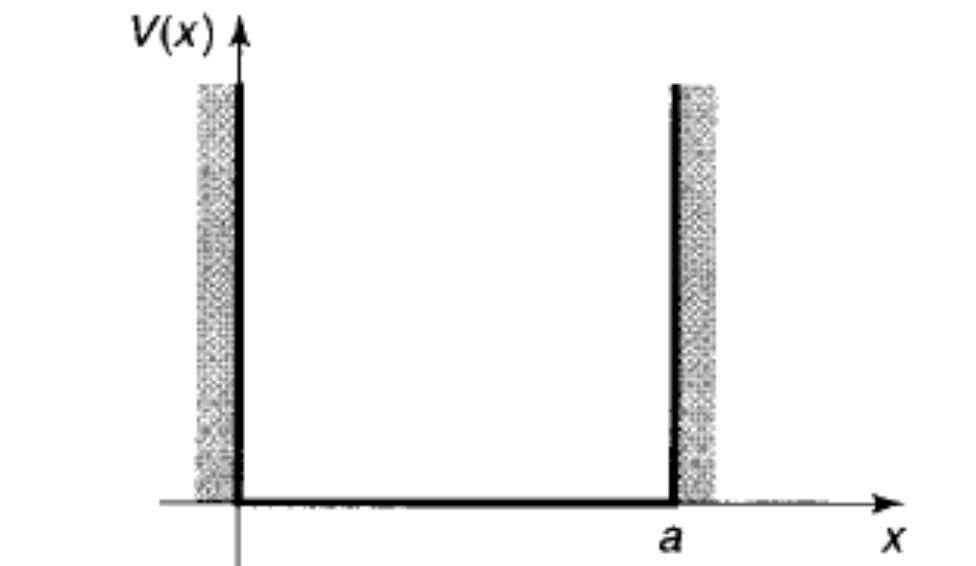
假设：

V(x)={0,0≤x≤a,∞,其它地方V(x) = \begin{cases} 0, & 0 \leq x \leq a, \\ \infty, & \text{其它地方} \end{cases}

一维无限深方势阱

在势阱内， V=0V=0 , 定态薛定谔方程为：

d2ψdx2=−2mEψℏ2=−k2ψ\frac{d^2\psi}{dx^2}=-\frac{2mE\psi}{\hbar^2}=-k^2\psi

一般解为：

ψ(x)=Asin⁡kx+Bcos⁡kx,k≡2mEℏ\psi(x)=A\sin kx+B\cos kx,~~k\equiv\frac{\sqrt{2mE}}{\hbar}

这里 AA ，和 BB 由边界条件确定。

ψ(x)\psi(x) 连续性要求 ψ(0)=ψ(a)=0\psi(0)=\psi(a)=0 ，代入可得 B=0B=0 。且要么 A=0A=0 为平庸解，要么 sin⁡ka=0\sin ka=0 ，即：

ka=0,±π,pm2π,±3π,...ka=0,\pm\pi,pm2\pi,\pm3\pi,...

k=0k=0 同样为平庸解，我们把负数项合并到 AA 中，得到可区分的解：

kn=nπak_n=\frac{n\pi}{a}

EE 的可能值便为:

En=ℏ2kn22m=n2π2ℏ22ma2E_n=\frac{\hbar^2k_n^2}{2m}=\frac{n^2\pi^2\hbar^2}{2ma^2}

一维无限深势阱的前三个定态

归一化 ψ\psi ( ϕ\phi 的模为 11 )：

∫0a∣A∣2sin⁡2(kx)dx=∣A∣2a2=1,所以∣A∣2=2a.\int_{0}^{a} |A|^2 \sin^2(kx) \, dx = |A|^2 \frac{a}{2} = 1, \quad \text{所以} |A|^2 = \frac{2}{a}.

AA 的相位无任何物理意义，我们可以简单地取正实根，阱内的解为：

ψn(x)=2asin⁡(nπax).\psi_n(x) = \sqrt{\frac{2}{a}} \sin \left( \frac{n \pi}{a} x \right).

解定态薛定谔方程会得到一个无限的解集（每一个正整数 nn 对应一个解）。ψ1\psi_1 具有最低的能量，称为基态；其它态的能量正比于 n2n^2 增加，称为激发态。函数 ψn(x)\psi_n(x) 的重要有趣性质：

  1. 它们相对于势垒的中心是奇偶交替的：ψ1\psi_1 是偶函数，ψ2\psi_2 是奇函数，ψ3\psi_3 是偶函数，依次类推。
  2. 随着能量的增加，态的节点（与 xx 轴交点）数逐次增加 1；ψ1\psi_1 没有（端点不计），ψ2\psi_2 有一个，ψ3\psi_3 有两个，依次类推。
  3. 它们是相互正交的，也就是说当 m≠nm \neq n 时

∫ψm∗(x)ψn(x)dx=0.\int \psi_m^*(x) \psi_n(x) \, dx = 0.

正交性证明

证明：

c∫ψm∗(x)ψn(x)dx=2a∫0asin⁡(mπxa)sin⁡(nπxa)dx=1a∫0a[cos⁡((m−n)πxa)−cos⁡((m+n)πxa)]dx={1(m−n)πsin⁡((m−n)πxa)−1(m+n)πsin⁡((m+n)πxa)}∣0a=1π{sin⁡[(m−n)π](m−n)−sin⁡[(m+n)π](m+n)}=0.\begin {aligned}{c} \int \psi_m^*(x) \psi_n(x) \, dx &= \frac{2}{a} \int_0^a \sin \left( \frac{m \pi x}{a} \right) \sin \left( \frac{n \pi x}{a} \right) dx\\ &= \frac{1}{a} \int_0^a \left[ \cos \left( \frac{(m-n) \pi x}{a} \right) - \cos \left( \frac{(m+n) \pi x}{a} \right) \right] dx\\ &= \left\{ \frac{1}{(m-n) \pi} \sin \left( \frac{(m-n) \pi x}{a} \right) - \frac{1}{(m+n) \pi} \sin \left( \frac{(m+n) \pi x}{a} \right) \right\} \Bigg|_0^a\\ &= \frac{1}{\pi} \left\{ \frac{\sin[(m-n)\pi]}{(m-n)} - \frac{\sin[(m+n)\pi]}{(m+n)} \right\} = 0.\\ \end {aligned}

注意上述证明对于 m=nm=n 不成立。（你能否找出问题所在？）在这种情况下，归一性告诉我们积分应该等于 1。事实上，我们可以把正交性和归一性写在一起：

∫ψm∗(x)ψn(x)dx=δmn.\int \psi_m^*(x) \psi_n(x) \, dx = \delta_{mn}.

这里的 δmn\delta_{mn}（所谓的 Kronecker delta 符号）是这样定义的，

δmn={0,如果m≠n1,如果m=n\delta_{mn} = \left\{ \begin{aligned} & 0, \quad \text{如果 } m \neq n \\ & 1, \quad \text{如果 } m = n \end{aligned} \right.

我们说它们是正交的。

  1. 它们还是完备的，也就是说任意一个函数 f(x)f(x)，都可以用它们的线性组合来表示：

f(x)=∑n=1∞cnψn(x)=2a∑n=1∞cnsin⁡(nπxa).f(x) = \sum_{n=1}^{\infty} c_n \psi_n(x) = \sqrt{\frac{2}{a}} \sum_{n=1}^{\infty} c_n \sin \left( \frac{n \pi x}{a} \right).

系数求法

上式其实就是 f(x)f(x) 的傅立叶展开，任何函数 f(x)f(x) 都可以用这种方法展开，称为 Dirichlet 定理。

在上式两端同乘以 ψm∗\psi_m^*，然后积分。

∫ψm∗(x)f(x)dx=∑n=1∞cn∫ψm∗(x)ψn(x)dx=∑n=1∞cnδmn=cm.\int \psi_m^*(x) f(x) \, dx = \sum_{n=1}^{\infty} c_n \int \psi_m^*(x) \psi_n(x) \, dx = \sum_{n=1}^{\infty} c_n \delta_{mn} = c_m.

（通过 δmn\delta_{mn} 把除了 n=mn=m 以外的项消除）。这样 f(x)f(x) 展开式中的第 nn 个待定系数就是

cn=∫ψn∗(x)f(x)dx.c_n = \int \psi_n^*(x) f(x) \, dx.

以上四个性质非常有用，而且它们不止是一维无限深方势阱所特有的。只要势垒对称就具备第一个性质；第二个性质是普遍适用的，无论势垒是什么形状都成立。正交归一性也是相当适应的一条结论，在零空间曲面叫 ortho-normality。完备性对你遇到的所有有势垒的情况都成立，且其证明比较巧妙。

得到一维无限深方势阱的定态：

Ψn(x,t)=2asin⁡(nπxa)e−i(n2π2ℏ/2ma2)t.\Psi_n(x,t) = \sqrt{\frac{2}{a}} \sin \left( \frac{n \pi x}{a} \right) e^{-i \left( n^2 \pi^2 \hbar / 2ma^2 \right) t}.

而含时薛定谔方程的最一般的解是定态解的线性组合：

Ψ(x,t)=∑n=1∞cn2asin⁡(nπxa)e−i(n2π2ℏ/2ma2)t.\Psi(x,t) = \sum_{n=1}^{\infty} c_n \sqrt{\frac{2}{a}} \sin \left( \frac{n \pi x}{a} \right) e^{-i \left( n^2 \pi^2 \hbar / 2ma^2 \right) t}.

通过选择适当的系数使之能拟合任何指定的初始波函数

通过选择适当的 cnc_n 使之能拟合任何指定的初始波函数 Ψ(x,0)\Psi(x,0)

Ψ(x,0)=∑n=1∞cnψn(x).\Psi(x,0) = \sum_{n=1}^{\infty} c_n \psi_n(x).

{ψn}\{\psi_n\} 的完备性（对现在的情况由 Dirichlet 定理证实）保证了总能用这种形式表示 Ψ(x,0)\Psi(x,0)，它们的正交归一性允许我们通过傅立叶技巧得到需要的待定系数：

cn=2a∫0asin⁡(nπxa)Ψ(x,0)dx.c_n = \sqrt{\frac{2}{a}} \int_0^a \sin \left( \frac{n \pi x}{a} \right) \Psi(x,0) \, dx.

也就是说：对于给定的一个波函数 Ψ(x,0)\Psi(x,0)，首先用上式求出展开式的系数 cnc_n，然后代入

Ψ(x,t)=∑n=1∞cn2asin⁡(nπxa)e−i(n2π2ℏ/2ma2)t.\Psi(x,t) = \sum_{n=1}^{\infty} c_n \sqrt{\frac{2}{a}} \sin \left( \frac{n \pi x}{a} \right) e^{-i \left( n^2 \pi^2 \hbar / 2ma^2 \right) t}.

得到 Ψ(x,t)\Psi(x,t)。

# 谐振子